The Melbourne CNRS Network (MCN) is a partnership between the University of Melbourne and the Centre National de la Recherche Scientifique (CNRS), France. It consists of researchers and joint PhD candidates from the University of Melbourne, the CNRS, and several French university partners.
At the heart of MCN sits a collective of collaborative researchers who share knowledge and resources to deliver high-quality research outcomes. The Network provides internal mentorship, inclusive peer support, as well as professional development and international networking opportunities for its members.

Our partner: CNRS
The CNRS is the national scientific research organisation in France. Its mission is to produce research that contributes to the technological, social and cultural advancement of society. CNRS researchers have created an impact in biology, chemistry, physics and information sciences. They have contributed to projects such as the development of the InSight Mars lander (in collaboration with NASA) and the Deep Underground Neutrino Experiment.
CNRS university partners
Candidates enrolled in a joint PhD in the Melbourne CNRS Network will complete their PhD at the University of Melbourne and one of the following French partner universities. The French partner university where the candidate is enrolled will depend on their project and CNRS supervisor.
Experiencing research culture at two different universities is incredibly enticing, as researchers from different backgrounds provide unique points of view. Alex Verhoijsen, MCN joint PhD candidate
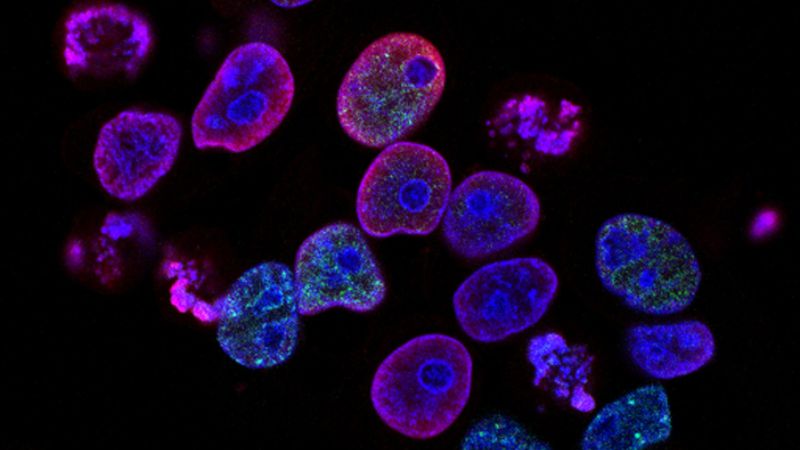
Project spotlight
Understanding colorectal cancer
Colorectal cancer (CRC) is one of the most common and lethal types of cancer, causing 935,000 deaths worldwide each year. Although treatments are available, patients often relapse after treatment has ceased. The ultimate cause of patient death is metastases forming in vital organs, such as the liver. Australian patients with metastatic CRC have a 5-year survival rate of only 13.4 per cent. To date, research has not provided an effective solution to prevent recurrence of CRC after treatment. This project aims to contribute towards solving the problem of cancer recurrence by examining the role of the protein netrin-1 and its receptors.
Meet our academic lead
Professor Frederic Hollande is the Academic Lead of the Melbourne CNRS Network. Fred is the Deputy Head of the Department of Clinical Pathology, and also works at the University of Melbourne Centre for Cancer Research, located within the Victorian Comprehensive Cancer Centre (VCCC). He was recruited as a CNRS Research Fellow in France in 1996 to study molecular mechanisms that underlie the progression of colon cancer. In parallel with his academic work, Fred co-founded and served as the joint-scientific director of a small biotech company that developed therapeutic monoclonal antibodies. The company was acquired by the French pharmaceutical company Servier in June 2011.

First published on 24 March 2022.
Share this article
Keep reading
-
International PhD opportunities
Discover the fully funded Joint PhD opportunities that are currently available with universities and research institutions around the world.
-
Find a supervisor or research project
Discover how to find a supervisor and learn how they can support your graduate research, or search available research projects.
-
Research degrees
Become a graduate researcher at the University of Melbourne.
-
Life as a researcher
Read the stories of current and past graduate researchers. Find out about their experiences at the University and where their degrees have taken them.